|
The Reservoir Flood Mapping specification 2016 (RFM16), and variants before it, advocate that inundation models are undertaken using a "flat roughness" approach. For a specification that also suggests a use of a 2 m resolution hydraulic grid based 2D model, this seems a bit inappropriate. This is in no way an attack on more detail: using the 2 m LIDAR products for England and Wales is a fantastic idea for inundation modelling and it works very well, however to suggest that fine resolution topography alone will improve our understanding of the flood plain dynamics would be incorrect. Hear me out. RFM16 suggests a Manning's n value of 0.1, which is accepted by the guidance to be a little on the high side to account for urban areas and wooded areas. A Manning's n value of 0.1 is actually broadly described as follows by Chow, 1959:
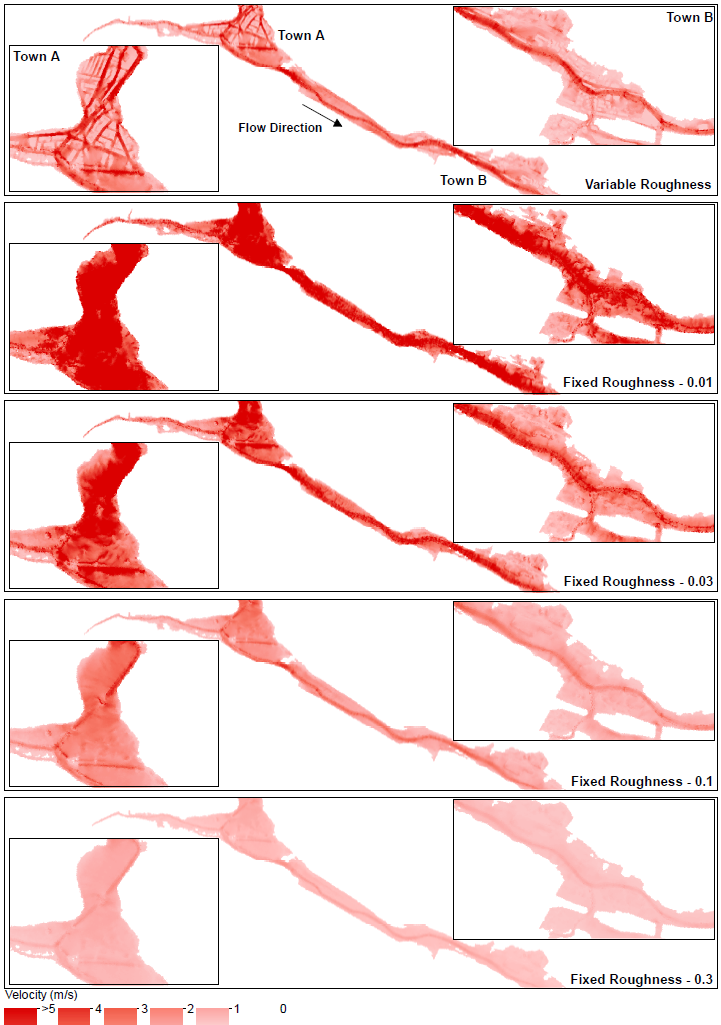
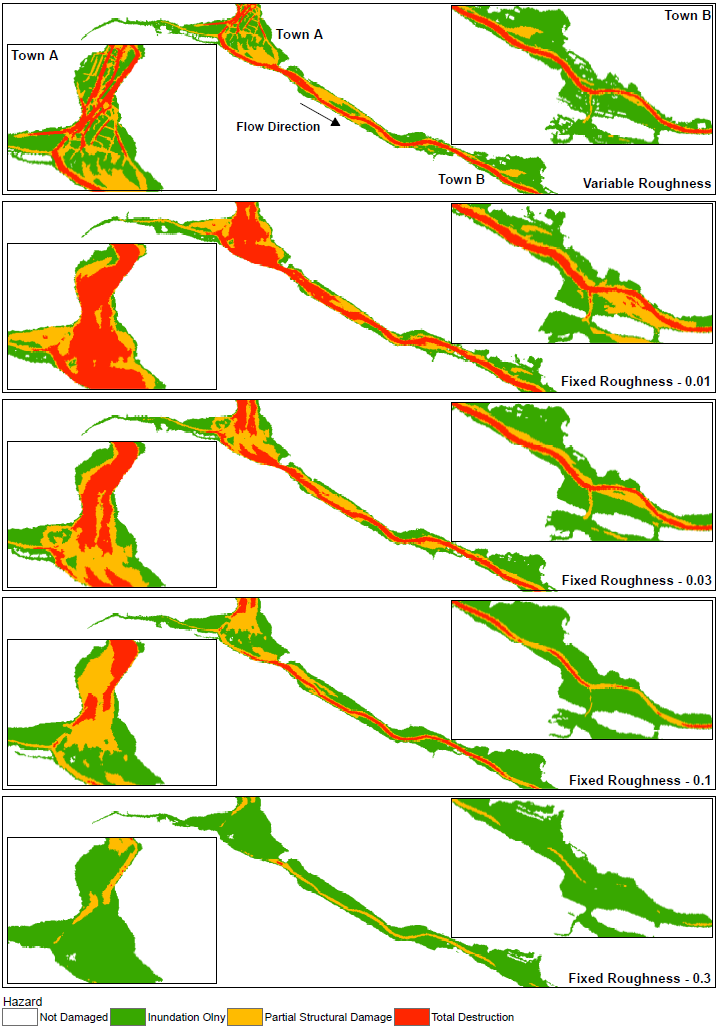
Without quoting the direct transport equations (because it isn't really important) it is important to understand that there are 2 underlying principles of shallow water equation models. The first is mass or volume conservation. This simply states that the volume in any control volume will increase or decrease as a function of the inflow and outflow, plus any effects from 'sources' (i.e. inflows and outflows from the domain which occur within the control volume). Roughness has no direct impact in these equations. It does instead appear in the second underlying principle: momentum conservation. Momentum conservation can be thought of as the fluid loading. A major component of this, as you may have guessed, is gravity. So if fluid depth is high on one side of the control volume, and fluid depth is low on the other - momentum will load the control volume in the net downstream direction. After this term there is a roughness term, and it looks a bit like this: Where F is force, V is a velocity vector, of which u and v are the x and y components respectively. H is the height of the fluid in the control volume. Manning's n is used in Lambda as follows: This tells us a few things. Firstly, if we carry H outside of lambda we retain a negative exponent: this means that in deep water roughness effects are reduced a little bit. This makes sense, since roughness is in effect a measure of the bed shear resistance of the fluid. A greater depth means an increased depth over which shearing can take place. But perhaps the most important thing to consider is Manning's n. Frictional loading is related to n squared. This means you cannot simply 'take an average value' to account for both rough and smooth values of roughness and expect to develop a good understanding of the resulting hydraulic regime. This is very important especially in dense urban areas where there is a steep gradient in roughnesses between smooth and open roadways, gardens and cultivated parks, and buildings (which can be modelled as high roughness). We put this to the test in a recent piece of research and demonstrated that while inundation depths are not particularly sensitive to roughness (since they do not play a major part in the volume conservation aspect of SWEs), velocities are. Velocities are so sensitive to roughness that they significantly distort the Depth Velocity product. This is something that we typically use in the dams industry to score both building damage and fatality rates. This means that by adopting a fixed value, especially of 0.1, you may significantly underestimate the number of fatalities and building damage/third party losses. We've shown that if you need to take a fixed value of roughness, a value somewhere between 0.035 and 0.1 will be most appropriate, and that 0.1 is too high. Ideally, you want to do a variable roughness model, and there are a number of reasons which suggest that a grid based 2D model might therefore not be the best approach (and that a Flexible Mesh model might instead be more appropriate).
Are you thinking about your dam break assessments, or some other type of rapid inundation model? CCH can help. We are very experienced with this type of modelling and have published works in this field related not only to roughness, but also novel applications of predictive breach models, stochastic and disaggregated life loss models, and fragility based building damage and loss modelling. |
Archives
November 2018
Categories |
Services |
Company |
|

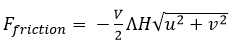
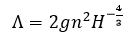
 RSS Feed
RSS Feed